Velocity variance of potential flow in a channel
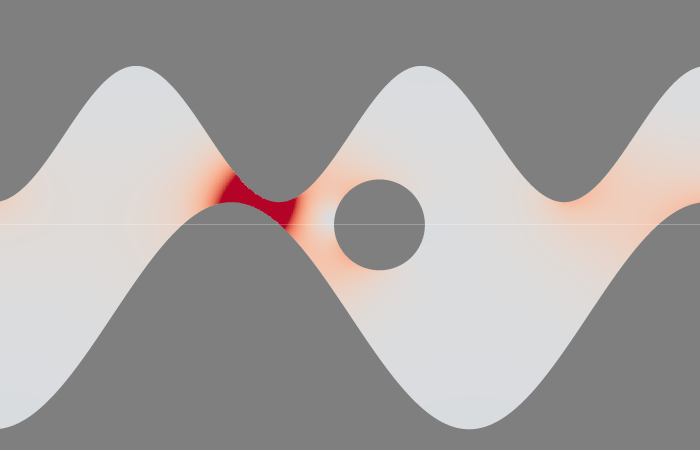
Consider incompressible potential flow () in a complex (no-penetration) geometry with an inlet and an outlet. At these locations, the potential-field value is set as a boundary condition with some difference . After solving the Laplace equation for the potential (), the total variance of the flow field () may be defined as the volume () integral , and the signed flux () as a surface integral of (say) the inlet area , , with the normal to the inlet plane. Given the system parameters and , we can define a single dimensionless number,
Intuitively, I assumed that this parameter could “summarize” the transport efficiency of a complex geometry by comparing the volumetric flow rate against the kinetic energy stored in the flow field. This should have be relevant for starting and/or pulsating flows. However, I found after some experimentation that this number is always , which I now understand.
Using the product rule for the inner product (), the fact that we study incompressible flow (i.e. ) and Gauss’s divergence theorem, we can rewrite the volume integral,
This surface integral only has contributions at the inlet and outlet, as the vector is parallel to on the channel’s walls. Such that,
which explains the unitary value for the aforementioned dimensionless ratio. Well done vector calculus for providing clarity on this topic!
But what does “summarize” a flowability of a complex geometry?
Say that for some non-zero value of , we have some total flux and variance . We can compute the volume flux per unit of energy of a flow field with a “Normalized” variance . This Omicron () value may be compared between various geometries to say something about their ability to facilitate flow with low kinetic energy.
Game of life on a sparse grid
I am currently starting to implement an adaptive Cartesian binary space partitioning (CBSP) mesh for a PDE-solver project. For this purpose I want to combine potentially small sections of Cartesian meshes of cells, where and can be two different powers of two. This entails a dynamic memory management such that only portions of the grid are allocated in memory. The movie below shows a Conway’s Game of Life session on a cells domain on such a grid. The color coding shows the allocated cells (Blue, magenta and green), the cells on which the game is played (magenta and green) and the cells that are “alive” (green). Meaning that no memory is allocated for the cells in the red region.
The memory management is performed using a pointer tree. In this example the data of a field is accessed via 32 pointers, each pointing up to 32 other pointers which could point to arrays of 8 cells. The (seemingly excessive) ratio of the number of pointers in the tree and the array size is tuned for the most convincing movie. The next admissible ratio in the code would be 16/32 as .
Code a flow solver
I have finished most of the writing for the simple flow solver pages. The purpose of these pages is to educate any body who is interested in the workings of flow-problem solvers. In fact, I actually coded this solver in basilisk before attempting to write a useful one.
Global temperature distribution
In preparation for a job interview, I made a movie which illustrated my so-called “research vision”. It is nice enough to share, and displayed below.
Paramo Sheffield
I invested some time in setting up a work bench for future DIY projects. For this purpose, I bought a small second-hand vice and gave it some tender love and care. Altough I tought I was finished, the Marktplaats.nl algorithm kept on pushing vice advertisements. When I came across the bigger brother of my (now) little vice, I knew it was meant to be…


The restoration entailed:
- Paint stripping
- Full decrease and clean
- Jaw-nut thread retreading
- Repaint
- Adding white highlights
- Soft-jaw upgrade(?) for the big vice.
Side note: The replaceable jaws are a joke. New jaws for the large one, cost more than an entire new vice (albeit made from Chinesium).
