Week 4A: Quaternions

You are already familiar with complex numbers: A quantity that consists of a real and an imaginary number. William Rowan Hamilton was already a well-established mathematician when he proposed to extend such complex numbers to quantities consisting of four components. A so-called quaternion () would consist of a real part and three imaginary parts
With the imaginary units satisfying . In a nutshell, these quaternions would be our algebraic structure of choice when working with Euclidean vectors and scalars. A vector would be written as a quaternion with a zero real part,
Interestingly, if you would multiply two vectors ( and ) represented as quaternions the Hamilton product would give you both the scalar product and the cross product.
Apart from the minus sign for the scalar product (inner product), it would allow for some neat vectorial algebra. For example, unlike the cross product, the Hamilton product is associative,
However, as you may have already realized, despite the efforts of Hamilton (Together with others such as Peter Tait) the quaternion system did not have enough compelling arguments to convince contemporaries such as Oliver Heaviside and Josiah Gibbs who were proponents of the vector algebra thought on this class. It may be instructive to realize that the vector algebra is not without its controversy (compare associative multiplication against the BACCAB rule), and if you find certain definitions not logical, than that is likely because they are not, they just happen to work well for some relevant applications.
Thank you history! for the interesting perspective.
Week 4A: A Leap into the deep

You have already seen how a vector-valued function can be used to describe lines in space. For example, a “Leap into the deep”-like structure can be described in cylindrical coordinates,
We can draw the local coordinate system as we “walk” over this line in positive direction.
But how is this useful? Well, consider the construction drawings of the actual artwork below.
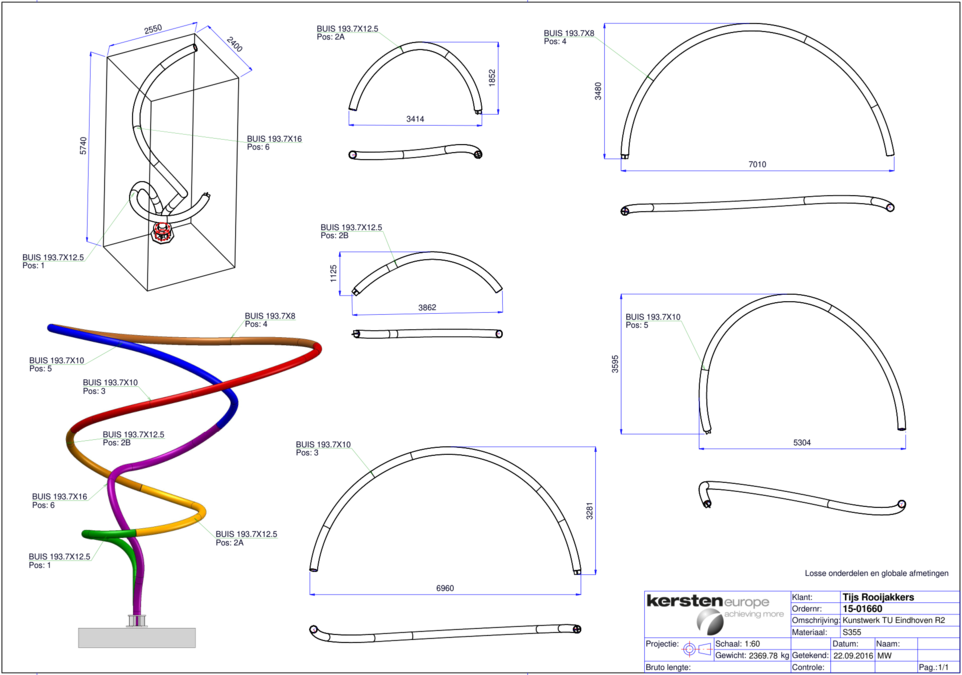
The curve is split into several sections that start out as a straight pipe. In a first step, the curvature is added. Curvature is inversely proportional to the radius of a local circle () fitted to the curve. It can be computed according to the Frenet-Serret formula,
Where and are the unit tangential and normal vector, respectively, is the intrinsic parameter, or the path length of the curve . So the curvature is a measure of how much the tangential vector moves in the direction of the normal direction per unit of length along the curve. After the pipes are bend, they will still lay flat on the floor. Some axial twist (i.e. so-called torsion ) is added, which can also be computed from the paramterization,
Indeed, the torsion is a measure for the movement of the binormal vector away from the (principal) normal vector.
Thank you local coordinate system and vector-function differentiation! for helping me describe these pipes.
Week 4B: Climbing the “Laplace tent”

On the Laplace square of our campus, i.e. near the parking space between the Traverse building and the Gemini building, sits an interesting tent-like structure. Upon close inspection is combines both circular and triangular arches into one structure. Say you want to climb this structure, but you first want to analyze your challenge. In order to make a proper free-body diagram to access the forces and their directions, you need to know the slope on various places on the roof. If you knew an expression for the unit normal vector (), one could compute the angle () with respect to the vertical direction , using the inner product,
We need some description of the surface. It turns out that is consists of four identical sections, the height () of the roof can be described with a functional relation in first quadrant using the coordinates drawn in the image.
with related to the radius of the aforementioned circular arch. We can compute two tangential vectors that span the tangent plane in .
The (not normalized) normal vector is perpendicular to this plane,
The unit normal is give by,
We can workout its z-component value (),
Which could be rewritten into a more compact form, but not by a lot. One can see that if we get , corresponding to and thus (One may stand straight up). However as the terms in the square roots become zero and , representing a vertical wall.
Thank you functions of multiple variables! for the help with climbing this structure.
