Antoon's site - LA and MC

home Blog Flow solver LA and MC Simulations W210 Recent activity

Week 3A: The vector space of polynomials.

Reconsider all polynomial functions of third degree $P_3$, an example of a function in this family is $y_1$,

$$y_1(x) = x^3 + 2x^2+3.$$

More generally, we can write a definition for $P_3$,

$$P_3=\{a_3x^3+a_2x^2+a_1x+a_0 \rvert a_3, a_2, a_1, a_0 \in \mathcal{R}\}.$$

Which motivates to introduce a vector notation,

$$\mathbf{a} = \begin{pmatrix}a_0\\a_1\\a_2\\a_3\end{pmatrix}.$$

But is it useful? It seems that if we say that our basis is $\{1, x, x^2, x^3\}$, we may write,

$$y_1(x) = x^3 + 2x^2+3 = \begin{pmatrix}3\\0\\2\\1\end{pmatrix}.$$

Furthermore, we can check the list of rules that a general vector space must obey. We will investigate some properties of scalar multiplication and polynomial addition to see what we are dealing with,

Lets define $y_2 = 2y_1 = 2x^3 + 4x^2 + 6 = \begin{pmatrix}6\\0\\4\\2\end{pmatrix}$, which is indeed part of our proposed vector space. We can quite safely infer from this example that scalar multiplication works “well” for any polynomial and scalar. What about addition? Lets say $y_3 = y_1 + y_2$,

$$y_3 = (1+2)x^3 + (2+4)x^2 + (6+3) = \begin{pmatrix}9\\0\\6\\3\end{pmatrix}.$$

Great succes! The coefficients of third-degree polynomials “act” as components of regular vectors, without introducing special rules for scalar multiplication and addition.

Now that we have the vector four dimensional vector space of $P_3$, we can also think of a the n+1 dimensional vector spaces associated with polynomnials of degree $n$ ($P_n$). It is clear that $P_3 \in P_4 \in P_5$, etc. A neat application if that we can describe differentiation as a linear map: $\frac{\mathrm{d}}{\mathrm{d}x}: P_m \rightarrow P_{m-1}$. For for the differentiation of a polynomial in $P_3$, we can write, $\frac{\mathrm{d}y}{\mathrm{d}x}: T(y) = Ay$ with $A$ and $3\times 4$ matrix.

$$A = \begin{pmatrix} 0 & 1 & 0 & 0\\ 0 & 0 & 2 & 0\\ 0 & 0 & 0 & 3\\ \end{pmatrix}.$$

For example

$$\frac{\mathrm{d}y_1}{\mathrm{d}x} = \begin{pmatrix} 0 & 1 & 0 & 0\\ 0 & 0 & 2 & 0\\ 0 & 0 & 0 & 3\\ \end{pmatrix}\begin{pmatrix} 3\\0\\2\\1\end{pmatrix} = \begin{pmatrix}0\\4\\3\end{pmatrix}=4x+3x^2.$$

Thank you vector spaces! for shining a new light on this topic.

Week 3B: Eigen vectors for describing the evolution of a dynamical system

Consider some infection disease affecting a population. We divide the population into healthy ($H$) and infected ($I$) people. Every day, 20% of the healthy people ($H$) are infected. However, thanks to a program organized by big pharmaceutical companies, 10% of the infected people become healthy again every day. We can write a population vector consisting of the number of healthy and infected people on day $n$ ($\mathbf{P}_n = \begin{pmatrix}H_n\\I_n\end{pmatrix}$). We can describe how $\mathbf{P}_{n+1}$ is related to $\mathbf{P}_n$ via a matrix equation,

$$\mathbf{P}_{n+1} = \begin{pmatrix}0.8 & 0.1\\0.2 & 0.9\end{pmatrix}\mathbf{P}_n$$

We can compute the eigen values and eigen vectors of this matrix,

$$\lambda_1 = 0.7$$

with,

$$\mathbf{v}_1 = \begin{pmatrix}1\\-1\end{pmatrix}$$

and

$$\lambda_2 = 1,$$

with,

$$\mathbf{v}_2 = \begin{pmatrix}1\\2\end{pmatrix}.$$

Can you see the meaning of $v_2$? Since $\lambda_2=1$, the vectors that are a multiple of $v_2$ are equilibrium points. We can also study how some example population evolves. Say we start with 90 healthy people and no infected ones ($\mathbf{p}_0 = \begin{pmatrix}90\\0\end{pmatrix}$). We may write the initial state as a sum of the eigen vectors (see figure), and find the solution.

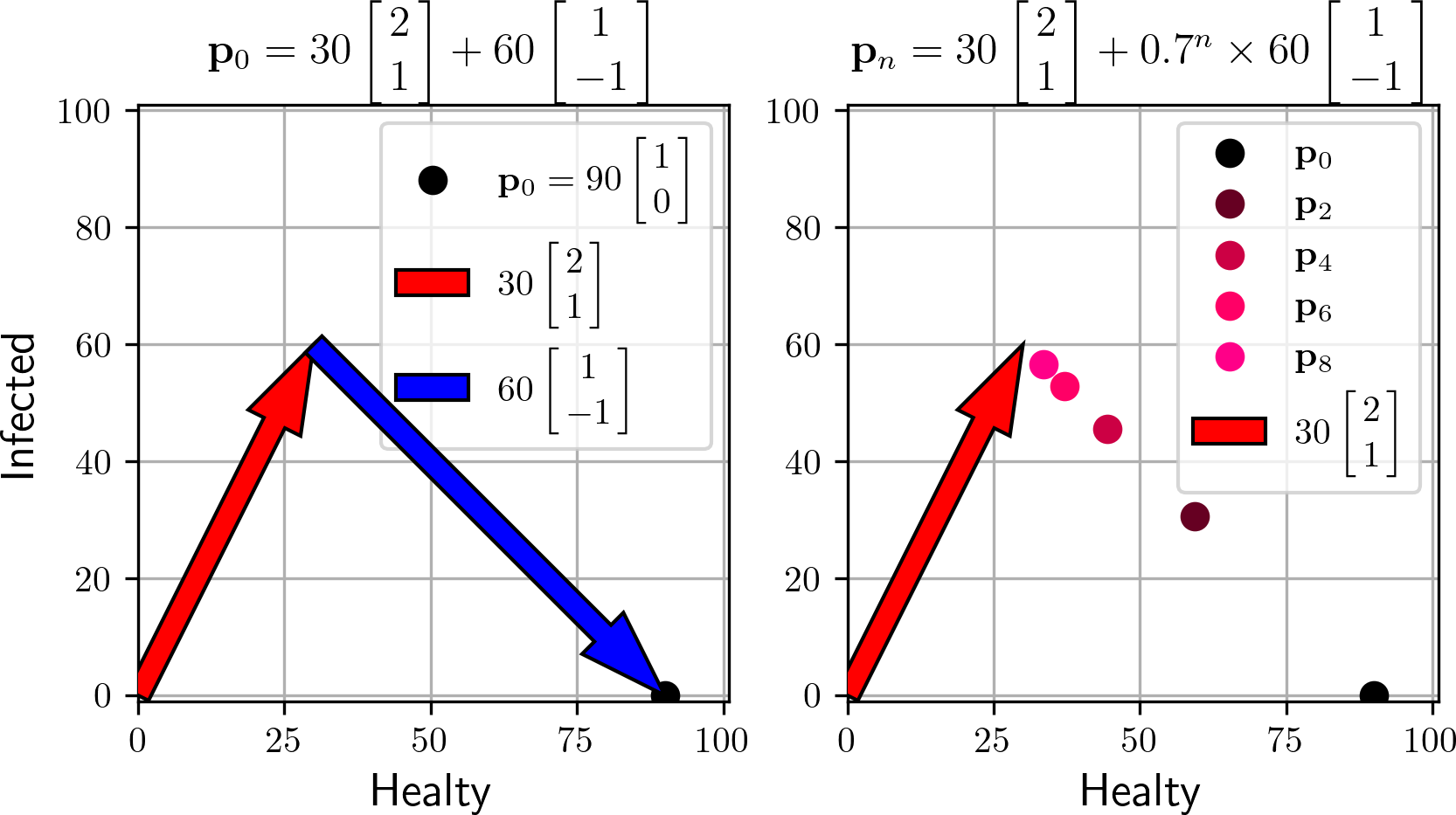
Alternatively, we can write the solution $\mathbf{p}_n$,

$$\mathbf{p}_n = \begin{pmatrix}0.8 & 0.1\\ 0.2&0.9\end{pmatrix}^n\mathbf{p}_0,$$

in a more attractive form using diagonalization,

$$\mathbf{p}_n = PD^nP^{-1}\mathbf{p}_0,$$

Where $P$ is the change-of-basis matrix consisting of the eigen vectors and $D$ the diagonal matrix with the corresponding eigen values.

$$\mathbf{p}_n = \begin{pmatrix}2&1\\1&-1\end{pmatrix} \begin{pmatrix}1&0\\0&0.7\end{pmatrix}^n \begin{pmatrix}\frac{1}{3}&\frac{1}{3}\\ \frac{1}{3}&-\frac{2}{3}\end{pmatrix} \mathbf{p}_0.$$

Thank you diagonalization! for this favorable form.

Continue to the example of week 4…